Tunnel ionization
Tunnel ionization is a process in which electrons in an atom (or a molecule) pass through the potential barrier and escape from the atom (or molecule). In an intense electric field, the potential barrier of an atom (molecule) is distorted drastically. Therefore, the length of the barrier that electrons have to pass decreases and electrons can escape from the atom (molecule) easily.
As an electric field of light is an alternating electric field, the direction of the electric field reverses after the half period of the field. Because electrons have a charge, electrons escaping by tunnel ionization come and go to the atom (molecule) in every half period. In this process, some electrons recombine with the nucleus (nuclei). Because the electrons have gained a large quantity of kinetic energy by acceleration from the electric field, surplus energy is released as light. The energy of this light is so high that this method is an effective way of generating ultraviolet light.
When the recombination does not occur, further ionization proceeds by collision between high-energy electrons and a parent atom (molecule). Consequently, a multivalent ion is created and this ion is collapsed by Coulomb repulsion. This is called Coulomb explosion.
Contents |
References and background
- The tunneling ionization rate for the hydrogen atom in an electrostatic field using the semi-classical approximation (L.D. Landau and E.M. Lifshitz, Quantum Mechanics (Pergamon, New York, 1965), 2nd ed., pg 276.)
- Tunnel Ionization probability for H-like atoms considering potential well was initially proposed by Keldysh (Sov. Phys. JETP, 1965).
- Theory extended to ionization from excited electronic states by Peremolov et al. (Sov. Phys. JETP, 1966).
- Modified for complex atoms and ions by Ammosov et al. (ADK, JETP, 1986).
- Tunneling Ionization of atoms was first observed experimentally by Chin et al. (J. Phys. B, 1985).
- Extensive comparison of ADK predictions have been done by many workers like Augst et al. (J. Opt. Soc. Am, 1991) etc.
- Theoretical and Experimental works regarding ionization related to advanced particle accelerators, fast-ignitor scheme of ICF are noteworthy.
The theoretical work of ADK is so far the most valid and highly appreciated theory.
Physical Process
Tunneling Ionization is a QM phenomenon; a non-zero probability event for observing a particle escaping from the deformed Coulomb potential barrier, obviously this phenomenon is forbidden by classical laws, as in the classical picture an electron does not have sufficient energy to escape.
As the Coulomb potential barrier is lowered, its width decreases, and this in turn increases the probability of electron tunneling through the barrier. The ADK probability formula gives the expression for the probability of tunnel ionization.
Notation
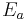 is the characteristic atomic electric field (the electric field at the bohr radius)
is the characteristic atomic electric field (the electric field at the bohr radius)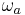 is the frequency associated with the ionization energy (i.e. the ground state energy)
is the frequency associated with the ionization energy (i.e. the ground state energy) is the applied electric field
is the applied electric field is the mass of an electron
is the mass of an electron is the electron charge
is the electron charge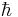 is the dirac constant
is the dirac constant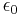 is the dielectric constant
is the dielectric constant
DC Tunneling Ionization
Tunneling ionization from the ground state of a Hydrogen atom in an electrostatic (DC) field was solved schematically by Landau.[1] This provides a simplified physical system that given it proper exponential dependence of the ionization rate on the applied external field. When 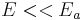 , the ionization rate for this system is given by:
, the ionization rate for this system is given by:
Landau expressed this in units where 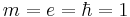 . In SI units the previous parameters can be expressed as:
. In SI units the previous parameters can be expressed as:
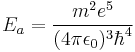 ,
,
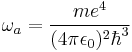 .
.
The ionization rate is the total probability current through the outer classical turning point. This is found using the WKB approximation to match the ground state hydrogen wavefunction though the suppressed coulomb potential barrier.
AC Electric Field
The ionization rate of an hydrogen atom in an alternating electric field, like that of a laser, can be treated, in the appropriate limit, as the DC ionization rate averaged over a single period of the electric fields oscillation. This models was proposed by Keldysh and then later expanded to hydrogen-like atom by A.D.K..
- ^ L.D. Landau and E.M. Lifshitz, Quantum Mechanics (Pergamon, New York, 1965), 2nd ed., pg 276.
![w = 4 \omega_a \frac{E_a}{\left|E\right|} \exp\left[ -\frac{2}{3}\frac{E_a}{\left|E\right|} \right]](/2012-wikipedia_en_all_nopic_01_2012/I/fa1962b2f3c11b78895af4f144ce4ec8.png)